フィボナッチ数列と黄金比(2006年04月09日)
先週の株式教室の「エリオットの波動論」の中でフィボナッチ数列という数の並びがでてきました。数列というとある規則にしたがって並んだ数字のことで、はるか昔の中学校の数学で習いましたね。
等差数列:2 5 8 11 14 17 20 23 26 29 32 35 ・・・
等比数列:2 4 8 16 32 64 128 256 512 1024 2048 ・・・
くらいは憶えているでしょう。等差数列は、隣り合う数字の差が一定(上の場合は3)の数の並び、等比数列は、隣り合う数字の比率が一定(上の場合は2) の数の並びです。
フィボナッチ数列というのは、もう少し複雑で、ある順番の数は、前の2つの数の和になる数列のことです。
フィボナッチ数列:1 1 2 3 5 8 13 21 34 55 89 144 233 377 ・・・
6番目の8は、その前の5と、そのまた前の3の和ですね。
この一見単純な規則の数列が、世の中のいろいろなものを表すのに適しているらしいのです。
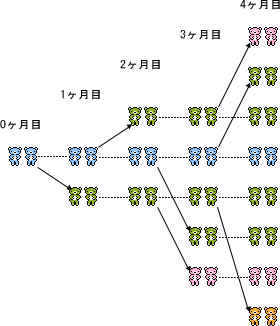
例えば、株式教室でもでてきたウサギの数の問題。
最初、生後1ヶ月の1組のウサギのつがいがいるとして、
(1)産まれたウサギのつがいは、2ヶ月後にウサギのつがいを産む
(2)2ヶ月後以降は、毎月1組のウサギのつがいを産む
という条件の場合(この際、ウサギの近親相姦については目をつぶります)
1年後には何組のウサギのつがいになっているでしょうか?という問題で、ウサギのつがいの増え方の規則をフィボナッチ数列で表すことができます。(右図)
1 2 3 5 8 13 21 34 55 89 144 233 と増えていき、12ヶ月後には377組のウサギのつがいに増えています。
今月、子供を産むのは、2ヶ月前にいたウサギのつがいのすべてですので、1ヶ月前のウサギのつがいの数に、2ヶ月前のウサギのつがいの数(今月子供を産むつがいの数)を足したものが、今月のウサギのつがいの総数になるという理屈ですね。
その他にも、松ぼっくりやひまわりの螺旋状に並ぶ各周回のつぶつぶの数の増え方とか木の枝の増え方もフィボナッチ数列の規則の性質を持つそうです。そしてこ自然界に潜むルールであるフィボナッチがエリオットの波動論の価格の目標値などを求める上で用いられているのです。
フィボナッチ数列は、ある順番の数値をその前の数値で割った値を並べていくと面白いことに気付きます。
3/2 = 1.5、5/3=1.6666...、8/5=1.6、13/8=1.625、21/13=1.61538...、34/21=1.61904...、55/34=1.61764...、89/55=1.61818...、144/89=1.61797...、233/144=1.61805...、377/233=1.618025...
数が大きくなるにしたがい、一般に黄金比と言われている数字、1.6180339887...、数学では、Φ(ファイ)と呼ばれる数値にどんどん近づいていきます。Φ(ファイ)は、π(パイ)の親戚みたいなもので、πと同じく、決して同じ数字が繰り返し現れない無理数のひとつです。
黄金比とは、一本の線を2つに分割したとき、長い方の線と短い方の線の長さの比率が、元の線と長さと長い方の線の長さの比率と同じになるとき、その比率を黄金比といいます。長い方の線÷短い方の線=1.6180339887...(=Φ)なるのが黄金比ですね。
長い方の線と短い方の線でできた長方形のことを黄金方形といい、人間が見て最も美しく感じる形になります。
トランプ、テレホンカード、クレジットカード、名刺、タバコの箱、マンガ本、パリの凱旋門、ギリシャのパルテノン神殿などみな黄金方形になっています。ミロのヴィーナスの各部位の比率も黄金比になっているそうです。
さて、この黄金比の値はどこかで見たことありませんか? 1.61805... という数値です。株の目標価格によく使われる係数として使われていますね。
エリオットの波動論だと、第二波の下値の目安は第一波の高値の0.618倍、第三波の目標値は第一波の1.618倍、第四波の調整は第三波の0.618 とかのに使われています。日本語でも3分の2押し(つまり0.666)などで使われてるのは黄金比に近い値です。
0.618 というのは黄金比(1.618)と違う値ではないかと思いますが、そこが黄金比の不思議なところで、黄金比の逆数(1をそれ自身の値で割った値)を計算すると、黄金比の少数点以下と全く同じ数値になるのです。電卓で計算してみて確かめてみて下さい。
1.61803... = 1 + 1/1.61803...
数って不思議ですね。しかも黄金比などというお金に関係する名前のついた数学の値を株式でも使っているなんて神秘でさえもあります。
デンの今日のTake IT Easy:フィボナッチ数列と黄金比は関連性があり、黄金比の値は、株価の目標値や調整率の目安に使われています。
レイジーの今日のおとぼけ:前々回買った貴金属の値段と前回買った貴金属の値段の合計したものが、次回買う貴金属の値段です。これが私の黄金比。散財万歳!
